Teaching for Mastery
Teaching for Mastery Approach
At St Barnabas School we believe that the most effective means of teaching mathematics is via the Teaching for Mastery Approach. The pedagogical foundation for the Teaching for Mastery Approach centres largely on the work of Rosenshine’s Principles of Direct Instruction. (Please see the St Barnabas Teaching and Learning Policy)
The principles of a Teaching for Mastery Approach are:
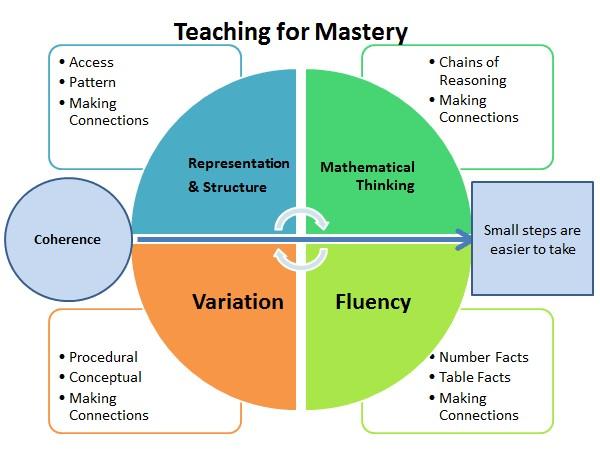
|
Coherence |
Representation and Structure |
Mathematical Thinking |
Fluency |
|
Lessons are broken down into small connected steps that gradually unfold the concept, providing access for all children and leading to a generalisation of the concept and the ability to apply the concept to a range of contexts. |
Representations used in lessons expose the mathematical structure being taught, the aim being that students can do the maths without recourse to the representation. |
If taught ideas are to be understood deeply, they must not merely be passively received but must be worked on by the student: thought about, reasoned and discussed with other. |
Quick and efficient recall of facts and procedures and the flexibility to move between different contexts and representations of mathematics |
|
Variation |
|
Variation is twofold. It is firstly about how the teacher represents the concept being taught, often in more than one way, to draw attention to critical aspects, and to develop deep and holistic understanding. It is also about the sequencing of the episodes, activities and exercises used within a lesson and follow-up practice, paying attention to what is kept the same and what changes, to connect the mathematics and draw attention to mathematical relationships and structure. |
We aim to equip all St Barnabas pupils with the mathematical skill, knowledge and understanding that they need to master the curriculum for each year group. As a result our curriculum demands that all pupils:
- recall key number facts with speed and accuracy and use them to calculate and work out unknown facts;
- develop their ability to apply mathematical skills with confidence and understanding when solving problems.
- apply their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions
- express themselves and their ideas using the language of mathematics with assurance.
- have sufficient depth of knowledge and understanding to reason and explain mathematical concepts and procedures and use them to solve a variety of problems.
- develop positive attitudes to mathematics, recognising that mathematics can be both useful and enjoyable.
- nurture a fascination and excitement of mathematics
- are able to use and apply the skills in other curricular areas.
Our expectation is that the majority of pupils will move through the programmes of study at broadly the same pace. However, decisions about when to progress should always be based on the security of the pupil’s understanding and assessment judgements made against ‘Ready to Progress’ criteria. Pupils who grasp concepts rapidly should be challenged through being offered rich and sophisticated problems before any acceleration through new content. Those children who are not sufficiently fluent with earlier materials should consolidate their understanding before moving on. Throughout the curriculum, a blended approach of keep up and catch up intervention is used.
